二叉树

概念

二叉树（英语：Binary tree）是每个节点最多只有两个分支(不存在分支度大于2的节点)的树结构。通常分支被称作“左子树”和“右子树”。二叉树的分支具有左右次序，不能颠倒。 – wikipedia

根节点：没有父节点的节点。一棵二叉树树只有一个根节点。
叶子节点: 没有子节点的节点，也叫终端结点。
层：指树的层次结构
满二叉树：每一个层次的节点数都达到最大值
完全二叉树:深度为k有n个节点的二叉树，当且仅当其中的每一节点，都可以和同样深度k的满二叉树，序号为1到n的节点一对一对应时，称为“完全二叉树”。(可以理解完全二叉树是满二叉树子集)
二叉查找树：左子树值小于节点值，节点值小于右子树节点值。

属性

第i层最多有2^(i-1)节点，深度为k的二叉树至多总共有2^(k+1)-1个节点数。

数据结构

public class BinaryNode<T extends Comparable> {
    public T data;// 节点值
    public BinaryNode<T> left;//左子树
    public BinaryNode<T> right;//右子树

    /**
     * data和左右子树构造节点
     *
     * @param data  节点值
     * @param left  左子树
     * @param right 右子树
     */
    public BinaryNode(T data, BinaryNode<T> left, BinaryNode<T> right) {
        this.data = data;
        this.left = left;
        this.right = right;
    }

    /**
     * data构造节点
     *
     * @param data 节点值
     */
    public BinaryNode(T data) {
        this(data, null, null);
    }
}

操作

定义BinarySearchTree实现二叉查找一些方法。

插入

插入思路比较简单，和节点比较，如果小于插入左边节点，如果大于插入右边，因为是从根节点开始，采用递归方式。

public void insert(T data) {
    if (data == null) {
        throw new RuntimeException("data is null");
    }
    root = insert(data, root);
}
private BinaryNode<T> insert(T data, BinaryNode<T> node) {
    if (node == null) {     //节点为空，则赋值
        node = new BinaryNode<T>(data);
    }
    int result = data.compareTo(node.data);
    if (result < 0) {       // 左
        node.left = insert(data, node.left);
    } else if (result > 0) {// 右
        node.right = insert(data, node.right);
    }
    return node;
}

递归思路很简单，按逻辑写下去，找到进入点、停止条件、返回值。

删除

删除操作有以下几种情况：

没有子节点：直接删除
有一子个节点：删除后子节点替代被删除节点位置
有两个子节点：找到右子树中最小节点，替换被删除节点(子树的最小节点替换时，也按照同样逻辑)

@Override
public void remove(T data) {
    remove(data, root);
}

private BinaryNode<T> remove(T data, BinaryNode<T> node) {
    if (node == null) {//结束条件: 未找到
        return node;
    }
    int result = data.compareTo(node.data);
    if (result < 0) {
        node.left = remove(data, node.left);
    } else if (result > 0) {
        node.right = remove(data, node.right);
    } else if (node.left != null && node.right != null) {// 找到对应值
        node.data = findMin(node.right).data;// 找到右子树最小值替换
        node.right = remove(node.data, node.right);
    } else {// 只有一个子
        node = (node.left != null) ? node.left : node.right;
    }
    return node;
}

找子树中最小节点(值)

递归左子树，左节点为空时，对应节点为最小节点,同样，最大子节点也类似。

public T findMin() {
    if (root == null) {
        throw new RuntimeException("root is null");
    }
    return findMin(root).data;
}

/**
 * 根据输入节点作为根节点查找树中最小节点
 *
 * @param node
 * @return 最小节点
 */
private BinaryNode<T> findMin(BinaryNode<T> node) {
    if (node == null) {
        throw new RuntimeException("Node is null");
    }
    if (node.left == null) {// (1). 左节点空，则最小
        return node;
    }
    return findMin(node.left);//(2). 不空，则递归
}

深度

深度，即二叉树有几个层级。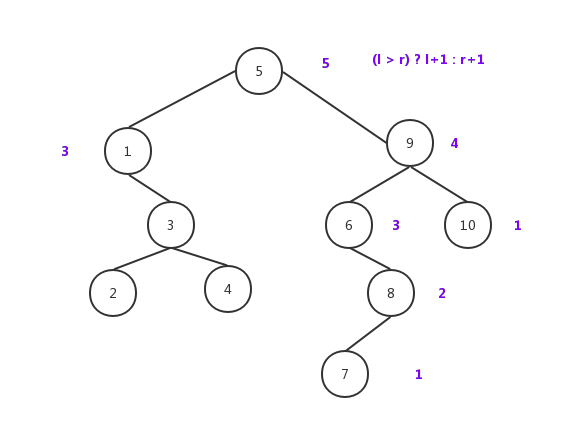递归遍历，子树比较后，大的值加1。如7，没有子节点，则为1，节点8左子树遍历返回值1，右子树返回0，结果是1+1=2.

private int height(BinaryNode<T> node) {
    if (node == null) {
        return 0;
    }else {
        int l = height(node.left);
        int r = height(node.right);
        return (l > r) ? l+1 : r+1;
    }
}

节点数size

节点数计算和深度类似，只是把左右节点累加，递归算法如下：

private int size(BinaryNode<T> node) {
    if (node == null) {
        return 0;
    } else {
        return size(node.left) + 1 + size(node.right);
    }

}

第K层的节点数

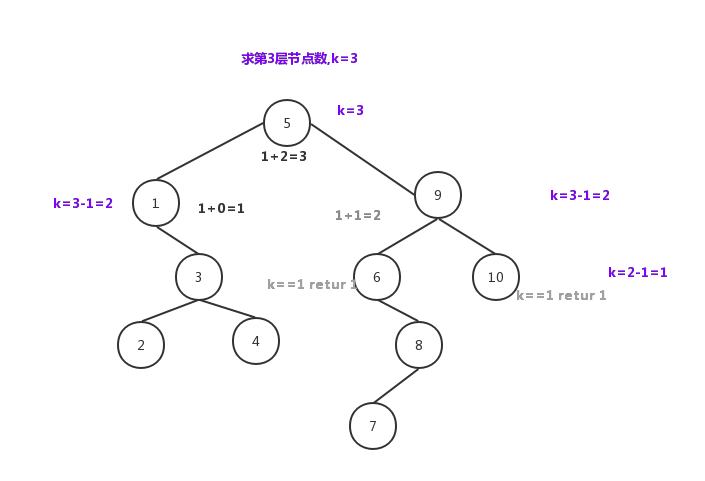如图，求3层节点数，从根节点遍历。子树为空返回0，否则一直k-1，直到k=1时返回1.再把左右遍历返回值相加。

 private int kSize(BinaryNode<T> node,int k) {
    if (node == null) {
        return 0;
    }
    if (k == 1) {
        return 1;
    }
    return kSize(node.left, k - 1) + kSize(node.right, k - 1);
}

判断两棵二叉树是否结构相同

递归比对节点，如果有一个节点为空，另一数的节点不为空，结构就不同。

public boolean compareTree(BinaryNode<T> node1, BinaryNode<T> node2) {
    if (node1 == null && node2 == null) {
        return true;
    } else if (node1 == null || node2 == null) {
        return false;
    }
    return compareTree(node1.left, node2.left) && compareTree(node1.right, node2.right);
}

求二叉树镜像

交换每个节点的左右子树即可，镜像后，中序遍历为逆序。

private void mirror(BinaryNode<T> node) {
    if (node == null) {
        return;
    }
    BinaryNode<T> temp = node.left;
    node.left = node.right;
    node.right = temp;
    mirror(node.left);
    mirror(node.right);
}

遍历

前序遍历

先访问根节点，再访问左子树，最后访问右子树。

private String preOrder(BinaryNode<T> subTree) {
    StringBuilder sb = new StringBuilder();
    if (subTree != null) {
        sb.append(subTree.data).append(" ");
        sb.append(preOrder(subTree.left));
        sb.append(preOrder(subTree.right));
    }
    return sb.toString();
}

中序遍历

先访问左子树，再访问根节点，最后访问右子树。二叉搜索树的中序遍历为 递增序列 。

private String inOrder(BinaryNode<T> subTree) {
    StringBuilder sb = new StringBuilder();
    if (subTree != null) {
        sb.append(inOrder(subTree.left));
        sb.append(subTree.data).append(" ");
        sb.append(inOrder(subTree.right));
    }
    return sb.toString();
}

算法题1：输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

知识点

前序遍历列表：第一个元素永远是【根节点 (root)】
中序遍历列表：根节点 (root)【左边】的所有元素都在根节点的【左分支】，【右边】的所有元素都在根节点的【右分支】

算法思路：

通过【前序遍历列表】确定【根节点 (root)】
【中序遍历列表】找root，找到后，根据root位置，把序列表分割成【左子数】和【右子树】；可知道，[左子树节点数量]
根据左子树数量，就可以再次把两个列表切分为左右子树，再递归；
如果出现指针交叉，退出递归。

public  TreeNode buildTree(int[] preorder, int[] inorder) {
    return buildTree(preorder, 0, preorder.length-1, inorder, 0, inorder.length-1);
}

private static TreeNode buildTree(int[] preorder, int preStart, int preEnd,int[] inorder,
    int inLeft, int inRight ) {
    if (preStart > preEnd || inLeft > inRight) {
        return null;
    }

    int rootValue = preorder[preStart];
    TreeNode node = new TreeNode(rootValue);
    int rootIndex = inLeft;
    for (int i = inLeft; i <= inRight; i++) {
        if (rootValue == inorder[i]) {
            rootIndex = i;
            break;
        }
    }
    int leftNodeSize = rootIndex - inLeft;
    node.left = buildTree(preorder, preStart + 1, preStart + leftNodeSize, inorder, inLeft, rootIndex - 1);
    node.right = buildTree(preorder, preStart + leftNodeSize + 1, preEnd, inorder, rootIndex+1, inRight);
    return node;
}

算法题2: 输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

class Solution {
    Node pre, head;
    public Node treeToDoublyList(Node root) {
        if(root == null) return null;
        dfs(root);
        head.left = pre;
        pre.right = head;
        return head;
    }
    void dfs(Node cur) {
        if(cur == null) return;
        dfs(cur.left);
        if(pre != null) pre.right = cur;
        else head = cur;
        cur.left = pre;
        pre = cur;
        dfs(cur.right);
    }
}

后序遍历

先访问左子树，再访问右子树，最后访问根节点。

private String postOrder(BinaryNode<T> subTree) {
    StringBuilder sb = new StringBuilder();
    if (subTree != null) {
        sb.append(postOrder(subTree.left));
        sb.append(postOrder(subTree.right));
        sb.append(subTree.data).append(" ");
    }
    return sb.toString();
}

特点：最后一个元素是根节点，而在根节点之前，可以分为两部分：左子树的节点值小于根节点值，右子树的节点值大于根节点值。

有根据此特性的逆向题目：输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

public class VerifyPostorder {

    public boolean verifyPostorder(int[] postorder) {
        return verifyPostorderHelper(postorder, 0, postorder.length - 1);
    }

    private boolean verifyPostorderHelper(int[] postorder, int start, int end) {
        if (start >= end) {
	        // 单个节点或空子树是二叉搜索树的后序遍历结果
            return true;
        }
		// 根节点的值为后序遍历的最后一个元素
        int root = postorder[end];
        int i = start;

        while (postorder[i] < root) {
	        // 找到第一个大于根节点值的索引，即右子树的起始位置
            i++;
        }

        for (int j = i; j < end; j++) {
            if (postorder[j] < root) {
	            // 右子树中存在小于根节点值的元素，不满足二叉搜索树的后序遍历结果
                return false;
            }
        }
		// 递归判断左右子树
        return verifyPostorderHelper(postorder, start, i - 1) &&
               verifyPostorderHelper(postorder, i, end - 1);
    }

    public static void main(String[] args) {
        VerifyPostorder solution = new VerifyPostorder();
        int[] postorder = {1, 3, 2, 6, 5};
        boolean result = solution.verifyPostorder(postorder);
        System.out.println(result); // Output: true
    }
}

层次遍历-BSF

按照层级从左到右遍历。这种遍历方式相对复杂，因为左右没有关联关系，只能一个个节点访问，按顺序把节点存起来，再从队列中取出节点访问其子树。可以通过一个FIFO队列实现。

其实这就是二叉树的 广度优先搜索（BFS），而BFS特性通常借助队列的先入先出特性来实现。

public String levelOrder() {
    LinkedBlockingQueue<BinaryNode<T>> queue = new LinkedBlockingQueue();
    StringBuilder sb = new StringBuilder();
    BinaryNode<T> tree = root;
    while (tree != null) {
        sb.append(tree.data).append(" ");
        if (tree.left != null) {
            queue.add(tree.left);
        }
        if (tree.right != null) {
            queue.add(tree.right);
        }
        tree = queue.poll();
    }
    return sb.toString();
}

分层打印还有其他变种题：

每一层打印为一行：遍历队列的时候，根据队列的size，打印一行。
之字形顺序打印二叉树：使用双端队列或者两个栈

二叉树中和为某一值的路径

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

解法：DFS+回溯，

前序遍历，把元素放入list，
并用targetSum-node.val;如果为0并且叶子节点，此时list正是所求路径；
如果不满足条件，回溯时，需要从队列删除元素

class Solution {
    LinkedList<List<Integer>> res = new LinkedList<>();
    LinkedList<Integer> path = new LinkedList<>(); 
    public List<List<Integer>> pathSum(TreeNode root, int sum) {
        recur(root, sum);
        return res;
    }
    void recur(TreeNode root, int tar) {
        if(root == null) return;
        path.add(root.val);
        tar -= root.val;
        if(tar == 0 && root.left == null && root.right == null)
            res.add(new LinkedList(path));
        recur(root.left, tar);
        recur(root.right, tar);
        path.removeLast();
    }
}

二叉树的最近公共祖先

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
	if(root == null || root == p || root == q) return root;
	TreeNode left = lowestCommonAncestor(root.left, p, q);
	TreeNode right = lowestCommonAncestor(root.right, p, q);
	if(left == null) return right;
	if(right == null) return left;
	return root;
}

参考: [1]. https://en.wikipedia.org/wiki/Binary_search_tree