Menu

Subscribe

B树和B+树

algorithm tree mysql

概述

之前文章中介绍二叉树和红黑树，红黑树解决树的平衡问题，避免二叉树退化为一个链表的情况，牺牲增删元素时保证树平衡的耗时操作，保证查询效率。 本文不深入实现，主要介绍B树和B+树为什么存在，应用场景是什么，为什么不能用红黑树代替？

什么是B树

先不解释B树的规则，否则容易头晕，我们先来看问题。红黑树查询效率已经很好了，特别是对于jdk8中HashMap中数据结构：首先，他为等值查找，不需要范围查找也不需要分组。其次，它都在内存里查找。

“内存”关键字很重要，如果数据存在磁盘上，每次节点对比查找，都涉及非顺序读的io操作，就比较耗时了，B树也正好为解决这个问题而来–更少的io操作。

磁盘读取数据是以盘块(block)为基本单位的。位于同一盘块中的所有数据都能被一次性全部读取出来。因此我们应该尽量将相关信息存放在同一盘块，同一磁道中，以求在读/写信息时尽量减少磁头来回移动的次数。

按顺序依次插入如下数据：

2,33,1,6,88,44,65,99,89,3,55,10,77

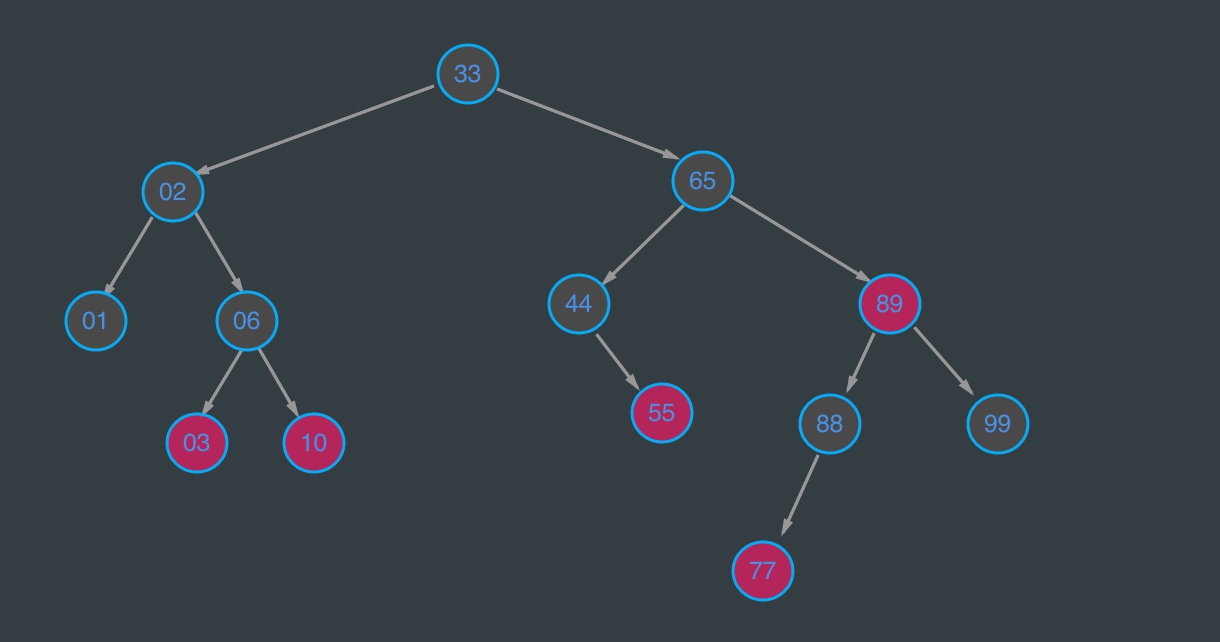
红黑树

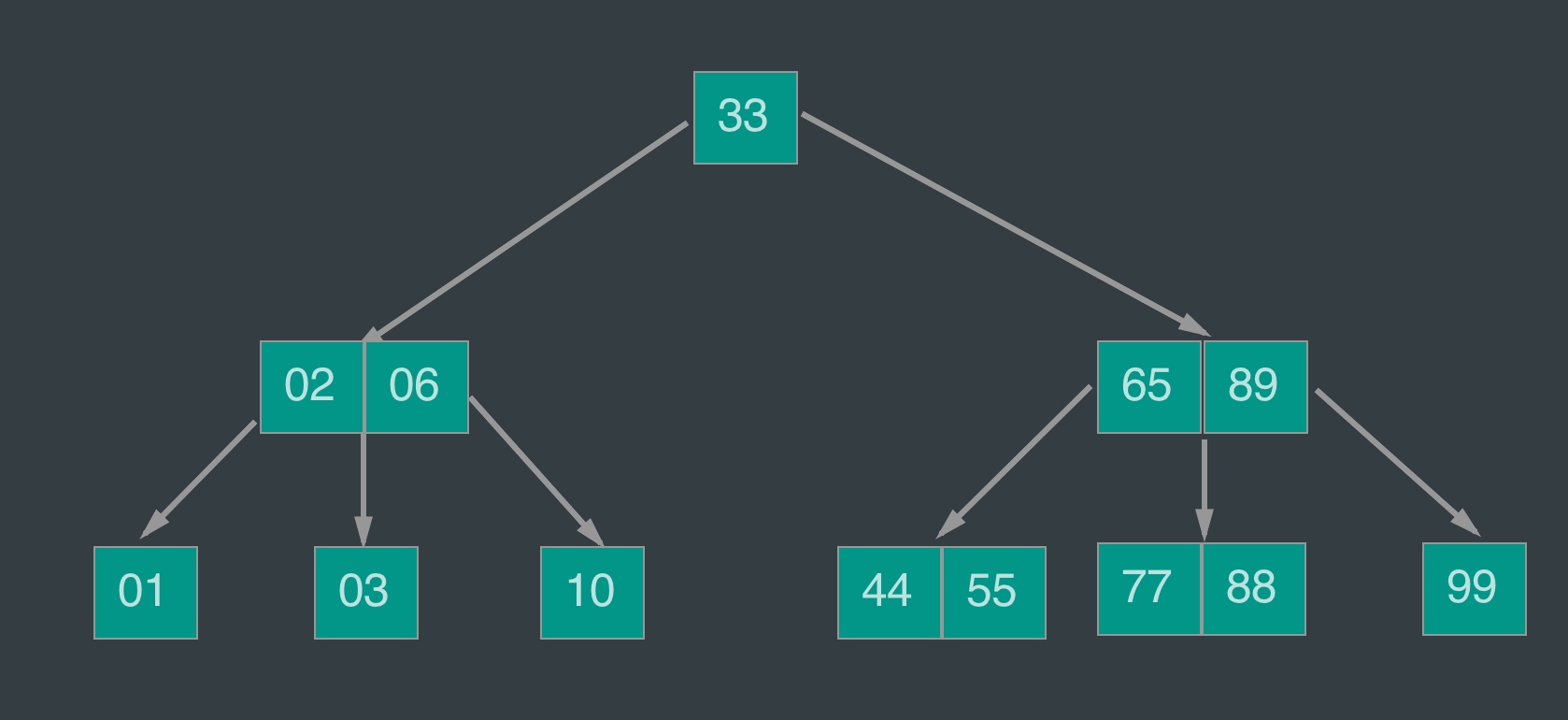
B树

可以看到B树和红黑树最明显的区别：

  • 不止两个儿子
  • 同一个节点上有多个元素

这两个特点意味着树的高度更小，如果每个节点是一个磁盘block，io读写移动次数更少。一个节点上多个元素一起读出来在内存查找，又一次减少了io访问次数。

比如图中红黑树查找88需要4次，而B树只需要3次即可。况且这是2元素3子节点的B树，如果数据量大、更多叉(阶)，优点更明显。当然也不是子节点越多越好，每个节点容纳的元素应该都在一个磁盘block上才能保证更少次数io访问。

下面我们再看B树的特点：

  1. 根结点至少有两个子女。
  2. 每个中间节点都包含k-1个元素和k个孩子，其中 m/2 <= k <= m。(也就是孩子数比元素多一个)
  3. 每一个叶子节点都包含k-1个元素，其中 m/2 <= k <= m
  4. 所有的叶子结点都位于同一层。
  5. 每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域分划(别被绕晕了，看一眼上图65-89和孩子的大小关系就清楚)。

m又叫阶，比如上图即一颗3阶的B树。元素个数最大2(k-1)，孩子数最大3(k<=m)

B+树

B+树是B树的变形，做了什么优化？

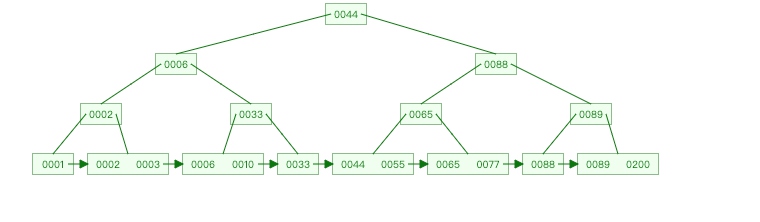可以看到，有重复元素，但叶子节点包含了所有节点元素，且除了叶子节点，其他节点并不保存具体元素对应的位置信息。什么意思，拿mysql存储来说，索引除了保存key，还需要保存对应数据位置才能定位到某条记录。 B+树在非叶子节不保存位置信息，意味着一个节点能存储更多元素，从而减少io次数。

这也意味着每个元素查找最后都要走到叶子节点才能拿到数据位置，但因此查询效率比较稳定。

从图中可以看到，叶子节点从小到大连起来，又解决B树遍历的效率和范围查询效率的问题。所以B+树比较适合作为关系型数据库存储数据结构。

先对B树特征如下：

  • 有n棵子树的结点中含有n-1 个元素；
  • 所有的叶子结点中包含了全部元素，及指向含有这些元素记录的指针，且叶子结点本身依元素的大小自小而大的顺序链接。

参考： https://www.cs.usfca.edu/~galles/visualization/BTree.html http://yangez.github.io/btree-js/ http://goneill.co.nz/btree-demo.php https://github.com/julycoding/The-Art-Of-Programming-By-July/blob/master/ebook/zh/03.02.md

CONTENTS