Menu

Subscribe

数据结构算法-3_排序

algorithm

本文总结一些经典的排序算法：

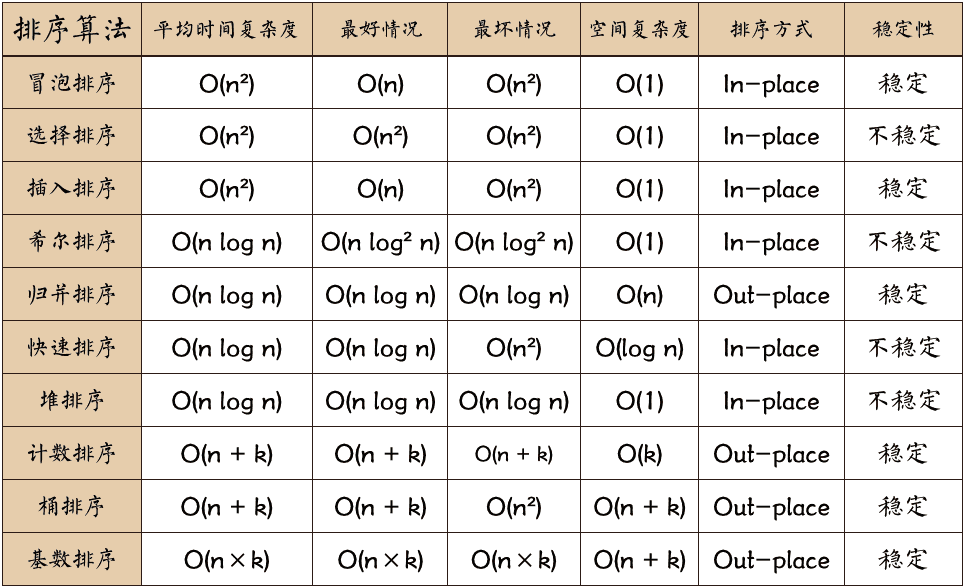
图片来源：https://github.com/hustcc/JS-Sorting-Algorithm

  • 内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。
  • 稳定性：排序后 2 个相等键值的顺序和排序之前它们的顺序相同，则稳定。

冒泡排序

描述：一种排序方式。遍历并对比相邻元素大小，交换位置，较大（小）逐步往后挪动。

  • 每次冒泡(遍历)：产生最大的元素，元素对比次数N-i(冒泡次数)
  • 冒泡次数：N-1
  • 对比元素个数

时间复杂度：O(N²)

代码：

public static int[] bubbleSort(int[] arr) {  
    int n = arr.length;  
    for (int i = 0; i < n - 1; i++) {  
        for (int j = 0; j < n - i - 1; j++) {  
            if (arr[j] > arr[j + 1]) {  
                // 交换 arr[j] 和 arr[j+1]                int temp = arr[j];  
                arr[j] = arr[j + 1];  
                arr[j + 1] = temp;  
            }  
        }  
    }  
    return arr;  
}

优化：

  1. 如果某次冒泡没有产生元素交换，说明已经排好序了。添加一个flag，用于终止冒泡。
  2. 记录每次冒泡终止的位置，说明后面的元素都是有序的，下次冒泡无需排序（可以替代1）。
  3. 双向冒泡排序；

插入排序

它的基本思想是：将待排序的数据分成两个部分，一部分为已经排好序的，另一部分为未排序的。初始时，已排序部分只有一个元素（通常是第一个元素），然后不断从未排序的部分中取出元素，并插入到已排序的部分的合适位置，使得已排序的部分仍然有序。

编程思路：

  1. 把第1个元素作为已排序，第2个之前的作为未排序分布；
  2. 从第2个开始，指针(i)遍历元素。每个元素插入左边（0~i-1）的合适位置；
  3. 由于插入数组需要移动之后的所有元素，所以从i-1最大的元素依次往左移动，如果大于要插入的元素，就往后移动一个位置，直到合适的位置。这样对比的同时完成了元素移动。
public void insertSort(int[] array) {
    for (int i = 1; i < array.length; i++) {
        int temp = array[i];
        int j = i - 1;
        // 这一步是实现原地排序的关键
        while (j >= 0 && array[j] > temp) {
            array[j + 1] = array[j];
            j--;
        }
        array[j + 1] = temp;
    }
}

时间复杂度为 O(n²)

优化：

  • 二分查找来确定插入位置。
  • 希尔排序（Shell Sort）：将数列按照一定的间隔分组，对每组使用插入排序，然后逐渐缩小间隔直到1，最终使整个数列有序。

插入排序vs冒泡排序

  • 时间复杂度也是O(n^2)，空间复杂度为O(1)，稳定的排序算法。
  • 内存交换：冒泡需要3次赋值，插入排序1次；

选择排序

每次从待排序的数列中选出最小（或最大）的一个数，将其放到序列的起始位置，直到全部排完为止。和插入排序的区别是，每次都从未排序列中找最小的元素。

时间复杂度为 O(n²)，不稳定。

归并排序(merge sort)

基本思想是：将待排序的数列不断地二分，直到每个子序列都只包含一个元素，然后将这些子序列合并成一个有序序列。合并的过程就是排序的过程。

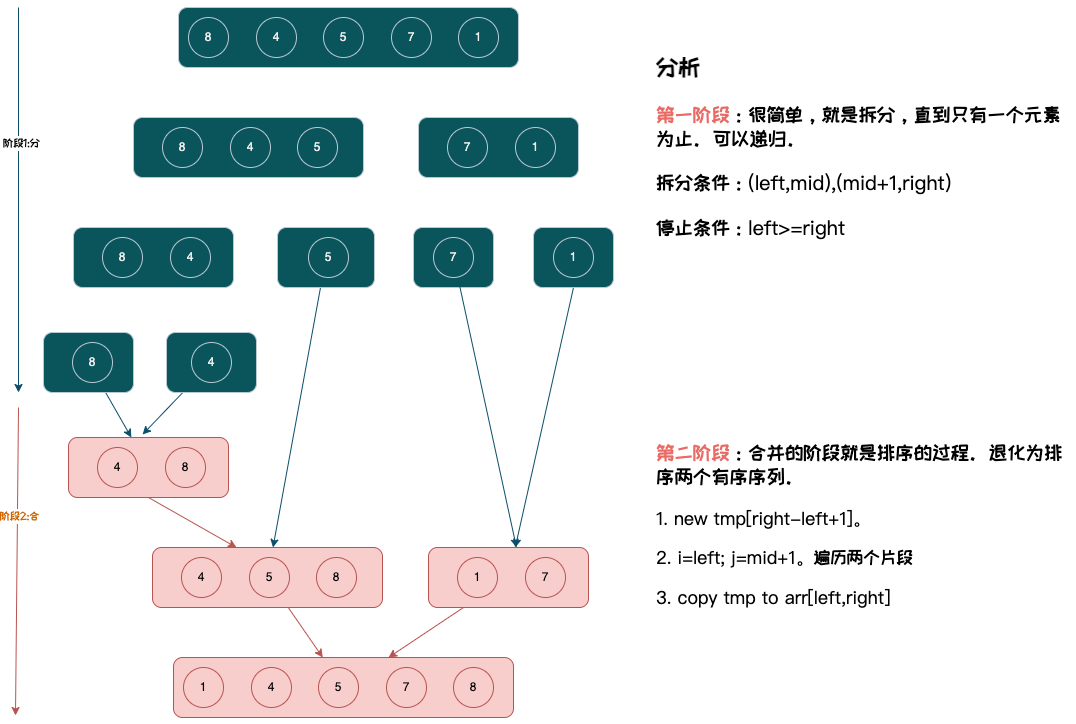
https://www.cnblogs.com/chengxiao/p/6194356.html

java实现

public static void mergeSort(int[] array) {  
    sort(array, 0, array.length - 1);  
}  
  
private static void sort(int[] array, int left, int right) {  
    if (left >= right) {  
        return;  
    }  
    int mid = (left + right) / 2;  
    sort(array, left, mid);  
    sort(array, mid + 1, right);  
    merge(array, left, right);  
}  
private static void merge(int[] arr, int left, int right) {  
    int mid = (left + right) / 2;  
    int[] tmp = new int[right - left + 1];  
    int i = left;  
    int j = mid + 1;  
    int k = 0;  
    // 对比两个片段并移动指针  
    while (i <= mid && j <= right) {  
        if (arr[i] <= arr[j]) {  
            tmp[k++] = arr[i++];  
        } else {  
            tmp[k++] = arr[j++];  
        }  
    }  
    // 没有遍历完成的继续追加  
    while (i <= mid) {  
        tmp[k++] = arr[i++];  
    }  
    while (j <= right) {  
        tmp[k++] = arr[j++];  
    }  
    // 拷贝tmp到源数组  
    for (int l = 0; l < k; l++) {  
        arr[left++] = tmp[l];  
    }  
}

优化：每次merge都要申请一次临时空间，为了降低开销，可以一开始就申请一个和源数组一样大的空间，给每一次merge使用。

特性：

  1. 稳定性: 是否稳定，需要看中merge中有没有改变等值元素顺序。如上代码，arr[i] <= arr[j])，保证了相同元素左边先放入tmp，所以可以做到稳定。
  2. 时间复杂度O(N*logN) ： N个元素：
  • 第一层：2个子区间，每个子区间数量为n/2
  • 第二层：4个子区间，每个子区间数量为n/4
  • 第三层：8个子区间，每个子区间数量为n/8
  • …
  • 第K层： N个子区间，每个子区间数量为1

所以：K = logN，也就是说，有N个元素，每次对半分开，需要分logN次（类似二叉树的深度），可以说切分的时间复杂度为O(logN)。

合并时，每次都会遍历所有元素，时间复杂度为O(N)，所以总的时间复杂度为 O(N*logN) 3. 空间复杂度 O(n) ： 需借助辅助数组实现合并，使用 O(n) 大小的额外空间；递归深度为 log⁡n ，使用 O(log⁡n) 大小的栈帧空间。 4. 非原地排序： 辅助数组需要使用 O(n) 额外空间。 5. 非自适应排序： 对于任意输入数据，归并排序的时间复杂度皆相同。

快速排序(quick sort)

基本思想：选取数组某个元素为基准数 ，将所有小于基准数的元素移动至其左边，大于基准数的元素移动至其右边。

编程思路：

  1. 选择基准数base，放左序列最后；
  2. 左指针(i)从left右移，大于等于base停止；（因为base中最右边，所以不会移除边界）
  3. 右指针(j)从right-1左移，小于base或者移到最左边停止；
  4. 左右指针停止后。
    • i<j：交换数据；继续移动指针，这样保证了i左边小于base，j右边大于base。
    • i>=j: 说明i左边<base,i和i右边大于等于base，此时i和base交换，完成数据分组。
  5. 使用i作为间隔，左右两部分继续充分1-4步。
public static void quickSort(int[] array, int left, int right) {  
    if (left >= right) {  
        return;  
    }
    int base = array[right];  
    int i = left;  
    int j = right - 1;  
    while (true) {  
        while (array[i] < base) {  
            // 左边指针往右边移动  
            i++;  
        }  
        while ( j > i && array[j] > base ) {  
            j--;  
        }  
        if (i < j) {  
            // 交换i j数据  
            int tmp = array[i];  
            array[i] = array[j];  
            array[j] = tmp;  
        }else {  
            // i >= j ：说明i是i左边最大的数值； 又因为i>=base，所以和base交换，完成所有数据分组  
            array[right] = array[i];  
            array[i] = base;  
            break;  
        }  
    }  
    quickSort(array, left, i - 1);  
    quickSort(array, i + 1, right);  
}

特性：

  1. 原地排序，不稳定。
  2. 最差O(N²)：每次分组，都是1和n-1个，时间复杂度O(N)，如果每次只有一个指针移动遍历N，平均遍历N/2，所以时间复杂度为O(N²)，也就是每次都取到最大值作为base的情况。
  3. 最优O(N*logN）：假设每次都是对半分，和归并差不多O(N*logN）。
  4. 平均时间复杂度O(N*logN）：假设每次分组对数1:9，比例为9这边：9N/10,9N/10²，…，1，$次数 = \log(10/9)^n$，去掉常量，也是logN.同样，主要分组的比例不随n的数量级变化，结果都是O(N*logN）。

优化：

  1. 性能的关键中于基准数选择，示例取最后一个，一种常见的优化方式是三数取中法；这样就可以在一定程度上避免最坏情况
  2. 对于小数组，快速排序比插入排序慢（5 ~ 15）。
  3. 如果数列里面大量重复元素：极端情况都是重复的，插入排序是O(N)，但快速排序还是O(NlogN)，

参考：

  1. 复杂度速查表
  2. 三种快速排序以及快速排序的优化
  3. 快速排序(Quick Sort)
CONTENTS