Menu

Subscribe

数据结构算法-4_堆heap

algorithm

定义

堆是一种特殊的树：

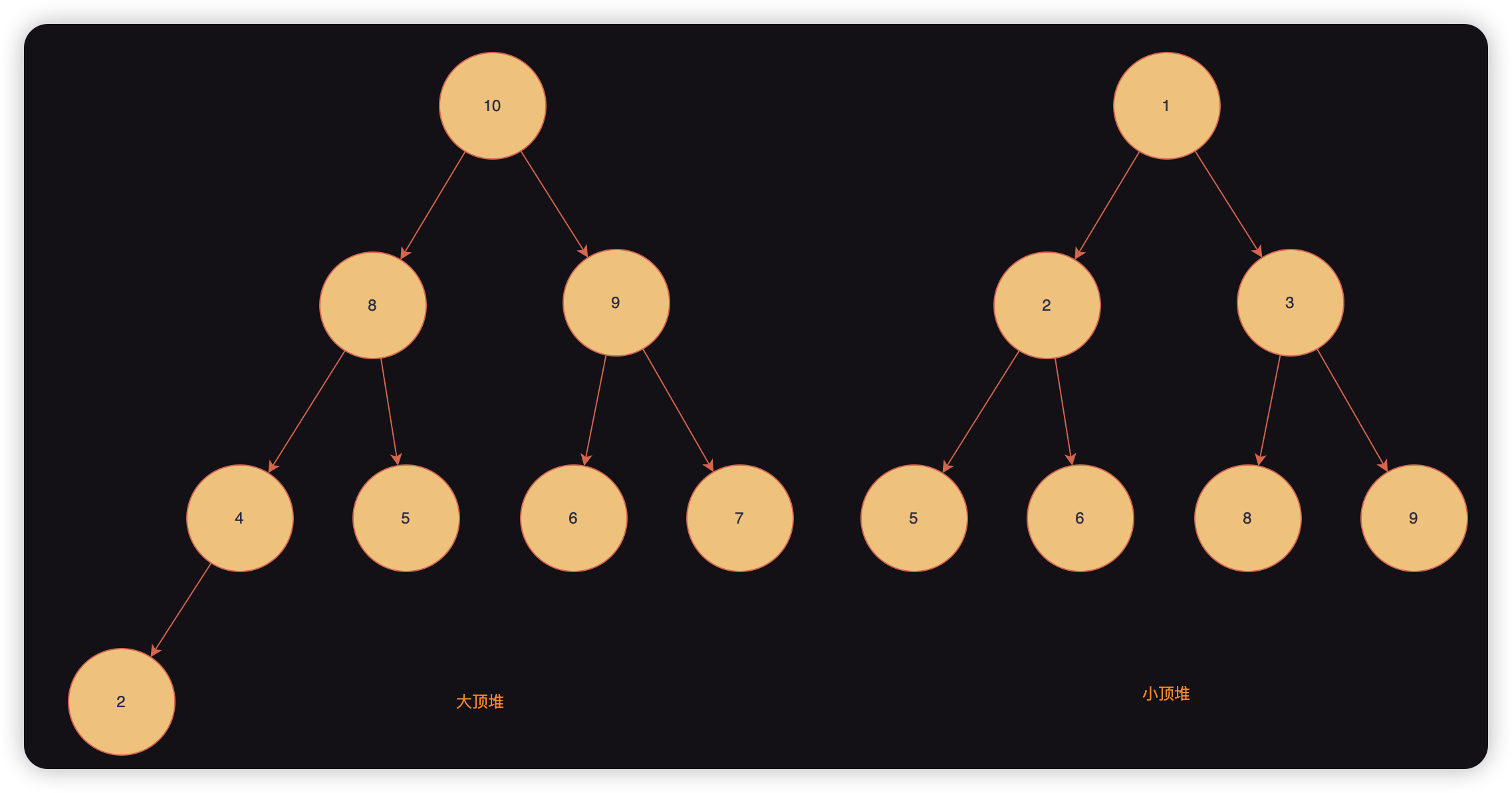
  1. 堆是一个完全二叉树。
  2. 堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值。大于叫大顶堆(此文以大顶堆为例)，小于叫小顶堆。

因为这两个特性，堆的查找效率很低，所以一般也不实现其查找元素。我们后面再讲其应用场景。先来看看图示： 完全二叉树适合用数组存储：如图2

  • 节点：下标i
  • 左节点：$i*2$
  • 右节点：$i*2+1$
  • 父节点：$i/2$
  • 第一个节点：array[1]

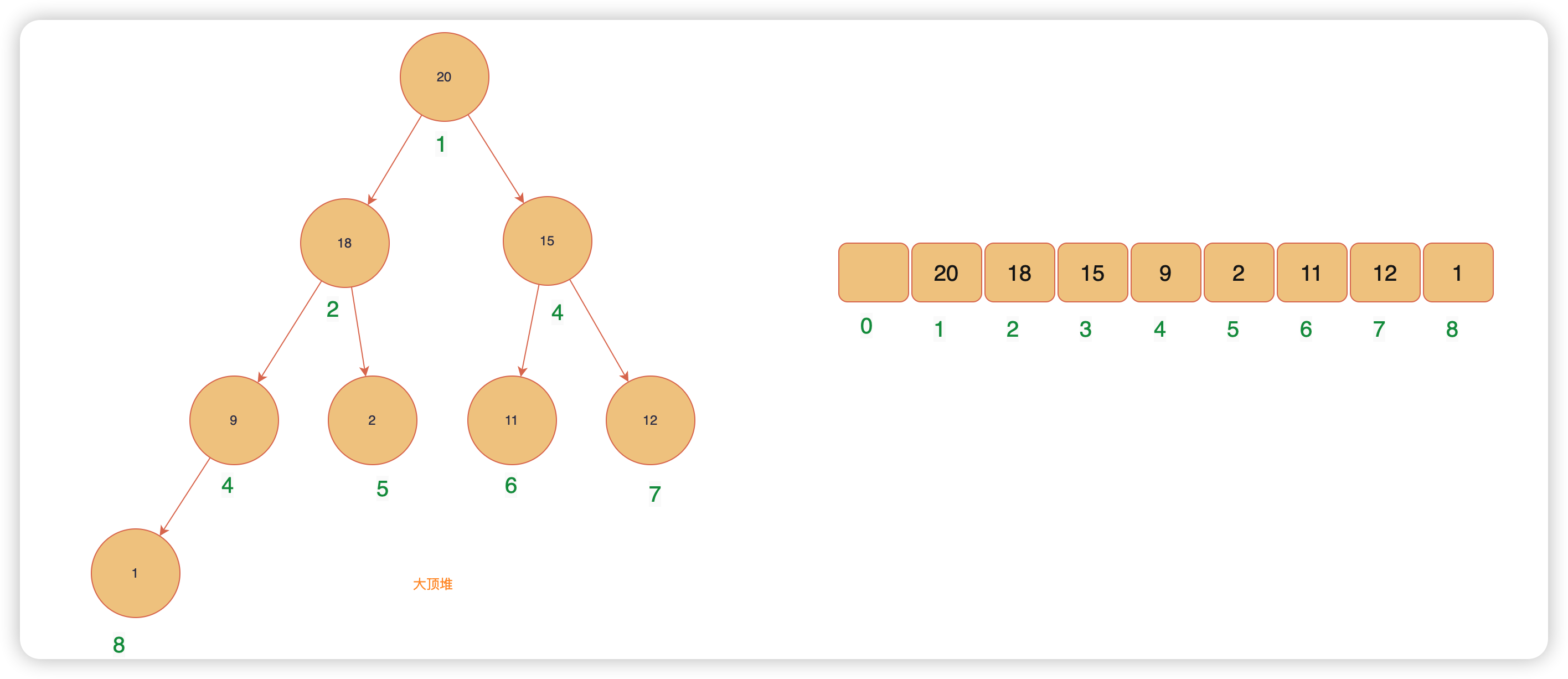
图2

实现

插入

思路：把插入的元素放在最后一个位置，再从下往上，和父节点对比，不满足特性就交换元素即可。

public class Heap {  
    private int[] a;  
    // 容纳元素个数  
    private int capacity;  
    // 当前元素数量  
    private int count;  
  
    public Heap(int capacity) {  
        a = new int[capacity + 1];  
        this.capacity = capacity;  
        count = 0;  
    }  
  
    private void insert(int data) {  
        if (count >= capacity) {  
            return;  
        }  
        count++;  
        // 先放中最后  
        a[count] = data;  
        int i = count;  
        while (i / 2 > 0 && a[i] > a[i / 2]) {  
            // 大于父节点  
            swap(a, i, i / 2);  
            i = i / 2;  
        }  
    }

时间复杂度：一个包含N个节点的完全二叉树，树的高度不会超过log2N，所以一复杂度为O($\log n$)

删除堆顶元素

思路：

  1. 删除堆顶，需要找到左右子最大的元素替换。被替换的元素作为顶，继续往下遍历删除。但会出现问题，可能不满足完全二叉树的条件；
  2. 删除堆顶元素，把最后一个元素替换到堆顶，然后『从上往下』对比交换元素，因为都是交换元素，不会出现某个叉空出来的情况，满足完全二叉树的特性。
public void removeMax() {  
    if (count == 0) {  
        return;  
    }  
    a[1] = a[count];  
    count--;  
    heapify(a, count, 1);  
}  
  
private void heapify(int[] a, int count, int i) {  
    while (true) {  
        int maxPos = i;  
        if (i * 2 <= capacity && a[maxPos] < a[i * 2]) {  
            maxPos = i * 2;  
        }  
        if (i * 2+1  <= capacity && a[maxPos] < a[i * 2+1]) {  
            maxPos = i * 2+1;  
        }  
        if (maxPos == i) {  
            break;  
        }  
        swap(a, i, maxPos);  
        i = maxPos;  
    }  
}

时间复杂度也是O($\log n$)

建堆

插入式建堆

先把已有数组按特性重新组织，也叫建堆，如果是从第一个开始读取元素，采用前面讲的插入的方法即可。

每个元素插入时间复杂度O(logN)，所以总时间复杂度为：O(N*logN) 。

如果是已经存在的数组，想原地(不需要new一个新数组存堆)建堆怎么做？也很简单，从下标为2的元素开始遍历，使用插入就行。如果是下标为i的元素，相当于i插入已经放中堆尾，然后就是往上(i/2)遍历交换元素,整个过程不影响i+1之后的元素。

从上往下

和删除堆顶的操作类似，从上往下看，保证左右节点小于自己。但因为此数组本身每堆化。如果从堆顶开始，1次遍历下来，只能保证路径上的元素满足条件。

换一种思路，如果从后往前遍历呢？

  1. 叶子节点：没有子，满足；
  2. 第一个非叶子节点a(兄弟为b)：对比两个子节点，和最大的元素替换，此时以a为顶的树满足堆的条件。
  3. 遍历到a的父节点A：因为a已经满足了堆的条件，如果A,a,b中a最大，和a交换元素。然后就相当于前面讲到的，删除堆顶a时最后一个元素替换上来的操作。

a-1,执行第3步直到堆顶即可。另外第一步每必要遍历，因为叶子节点天然满足条件。而完全二叉树，下标从n/2+1到 的节点都是叶子节点。于是只需要从n/2往前遍历即可。

private  void buildHeap(int[] a, int n) {  
    for (int i = n / 2; i >= 1; --i) {  
        heapify(a, n, i);  
    }  
}

时间复杂度: 简单分析：每个元素的堆化时间复杂度为O($\log n$)，需要堆化的元素 n/2 + 1个，去掉常量，所以时间复杂度为O(N*logN)，但实际上是O(N)，详见推到过程：

// TODO

插入式建堆

堆排序

建堆之后，如果是大顶堆，第一个元素就是最大的元素，把他和最后一个元素(n)交换，此时就类似删除堆顶元素的操作。完成后，又把堆顶和n-1的元素交换，直到只剩下一个元素。

时间复杂度：O(N)+ N* O(logN) = O(N*logN)

应用

  • 优先级队列
  • topK
  • 利用堆求中位数
CONTENTS