概述
二叉查找树的查找时间复杂度为O（lgN），但是二叉查找树有一个问题，如果插入的数据是有序的，就变成了一个链表，查找时间复杂度为O(N)。如下图1.1：
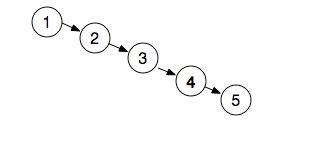图 1.1
为了解决这种退化的情况，需要对二叉树作平衡操作，但要保证二叉树的完全平衡的代价很高，因而演化出其他平衡树，比如2-3查找树，在一个节点上可能有2个键和3个链接，如下图1.2：8介于7和9之间，多了一条链。
图 1.2
2-3树很好地解决了保证平衡性的问题，但是代价也不小，比如查找就不如二叉查找树方便。还好，只需要作一点调整，就能很好地利用二叉查找树和2-3查找树的优点。我们用一条红色链连接两个 2-节点 表示一个 3-节点 ，如图1.3：
图 1.3
我们把这种2-3树的表示方式称为红黑树。每一个节点只有一个链接指向自己（如指向4的红色链接），把它的颜色保证到节点上，也就相当于给节点着色，这就是我们最常见的红黑树。
红黑树的性质如下:
- 任何一个节点都有颜色，黑色或者红色
- 根节点是黑色的
- 叶子节点：黑色的空节点（主要是为了简化红黑树的代码实现而设置的）。
- 父子节点之间（相邻）不能出现两个连续的红节点。
- 任何一个节点向下遍历到其子孙的叶子节点，所经过的黑节点个数必须相等
如下图1.4，如果按照1-8的顺序插入，不再是链表结构。
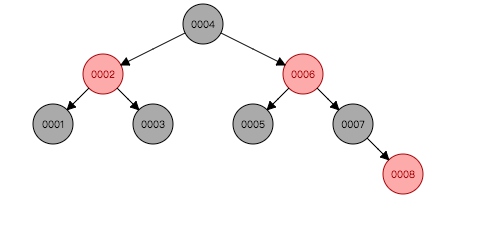图 1.4
总之，红黑树是一种平衡二叉查找树。它是为了解决普通二叉查找树在数据更新的过程中，复杂度退化的问题而产生的。红黑树的高度近似 logN，所以它是近似平衡，插入、删除、查找操作的时间复杂度都是 O(logn)。
二、插入
红黑树的插入和二叉搜索树一样，比对大小，找到节点插入。不同的是，插入后可能破坏了红黑树的特性，需进一步修复。新插入的节点，都作为红色处理(为什么是红色而不是黑色：黑色一定破坏性质的第四条，红色需要处理的情况简单一点)。
插入后不需要调整
- 如果是根节点，重新着色为黑即可。
- 父亲如果为黑色，并不违反红黑树性质，直接插入。
插入后需要调整
从上一种情况得知，插入后需要调整的，父节点一定是红色，又分3种情况。
3.1 叔叔节点为红色
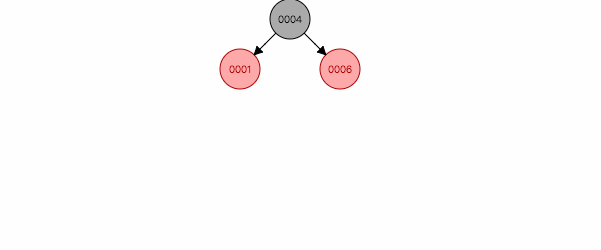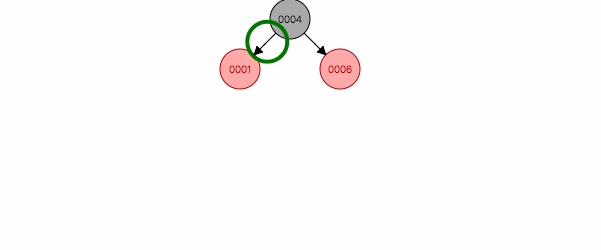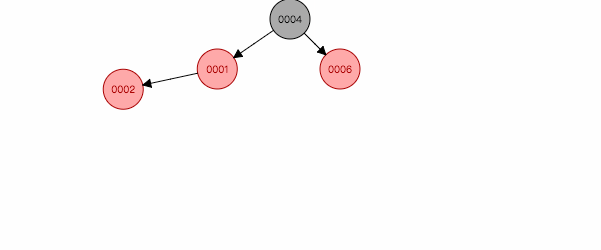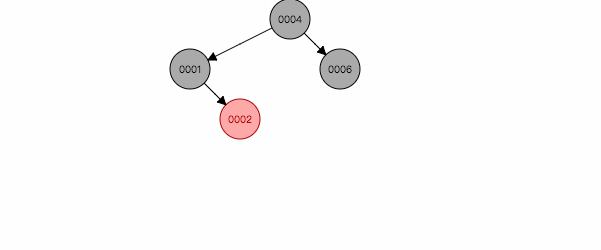图 2.1
父节点和叔叔都是红色，把他们都变为黑色，祖父变为红色，这样黑色节点同时减少一个，保证了特性5。
调整结束后，祖父节点又可能破坏特性4，继续按照插入的逻辑往上回溯。后续谈到的情况中，不再涉及递归回溯说明。即把修改后的节点(祖父)当成是新加入的节点进行各种情形的检查。 这就好比，二叉树remove()，删除一个节点，用子节点来替换，需继续删除用来替换的子节点，如此递归或循环。
3.2 叔叔节点为黑色(或空)，且祖父节点、父节点和新节点处于一条斜线上
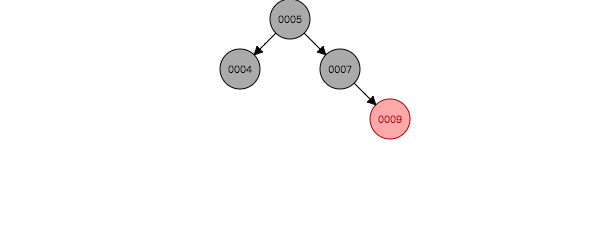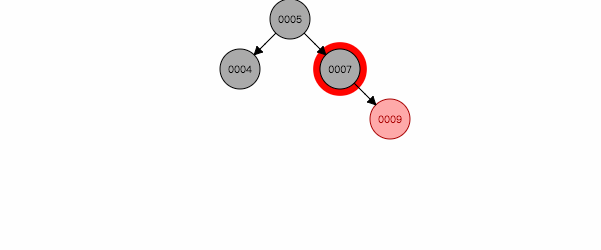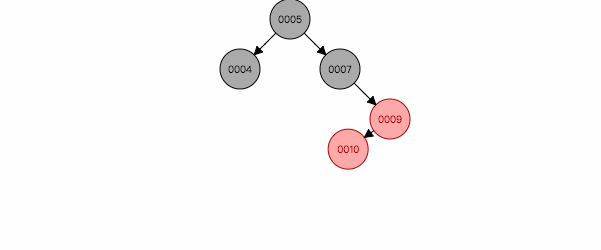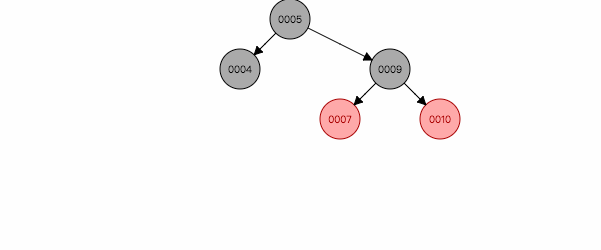图 2.2
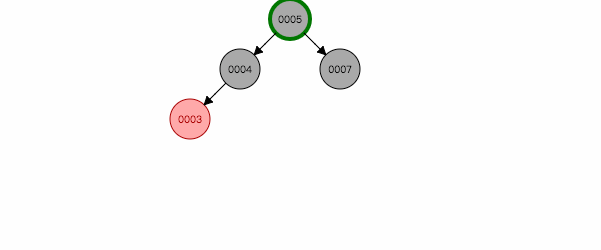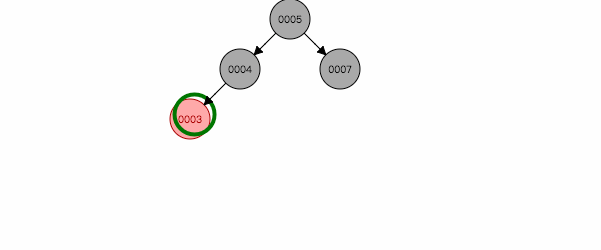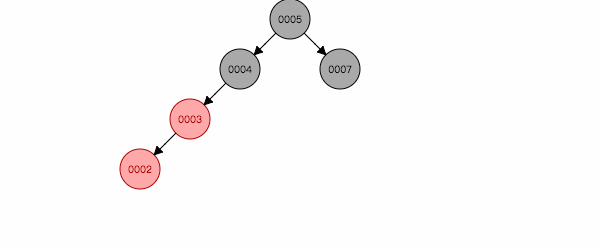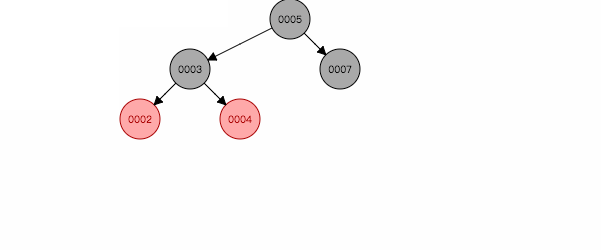图 2.3
如图2.2，在一条右斜线上，解决办法是：针对祖父节点7左旋，然后父亲祖父互换颜色。为什么这样能保证平衡性呢，因为祖父一定是黑色，旋转后，祖父位置被父亲替换，为了保证黑色节点不变少，父亲节点还用原来祖父的黑色。祖父旋转到另一个分支，黑色节点多了一个，重新着红色，同时保证了特性4，5。 反之为图2.4。
3.3 叔叔节点为黑色(或空)，且祖父节点、父节点和新节点不在一条斜线上
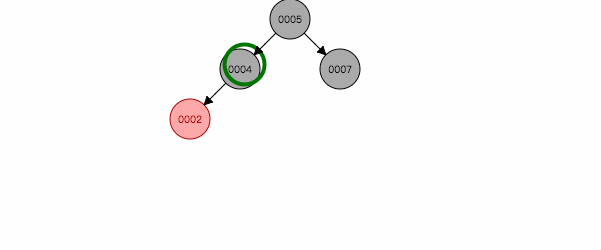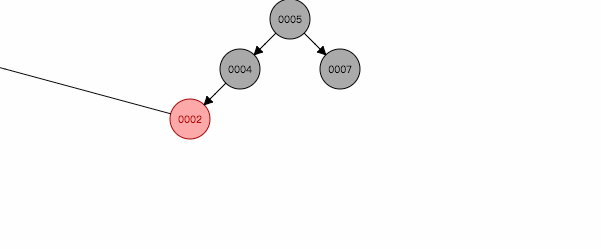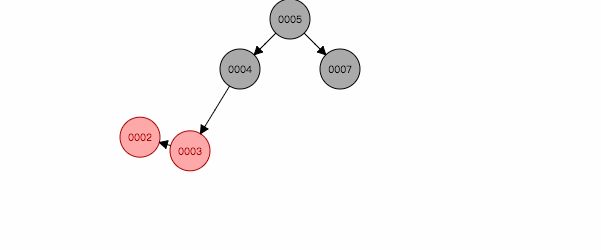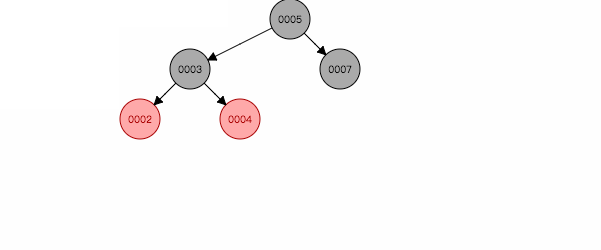图 2.4
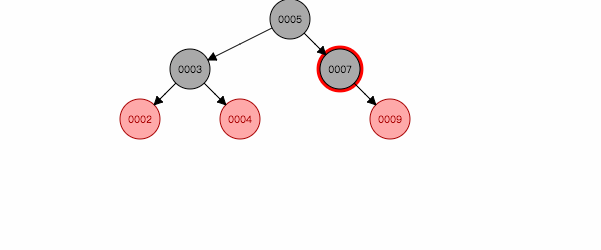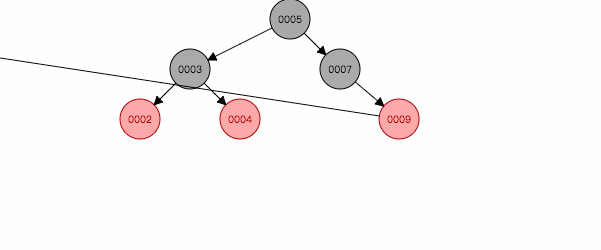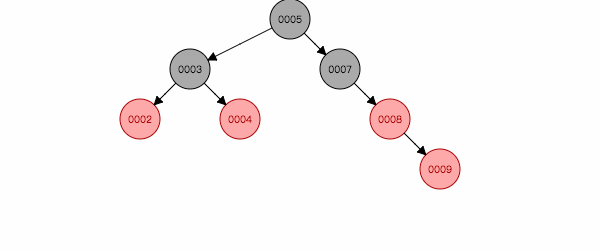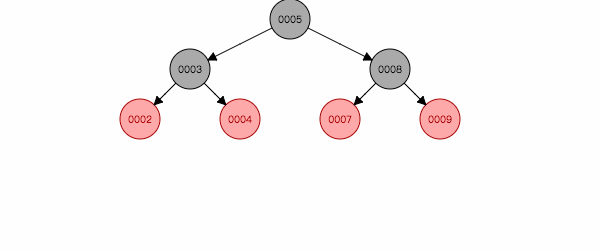图 2.5
如图2.4，插入节点3，左旋后，就跟第二情况类似，再按照第二种方式处理。反之亦然。
实现
要实现插入，先要实现几个方法，首先是能找到需要插入节点对应的父节点，插入后，需要找到叔叔节点。之后就是重新着色和左右旋。
/**
* 寻找父节点:
* 跟二叉查找树一样，比对节点值大小，找到要插入的父节点
*
* @param node node
* @return RBTreeNode node
*/
public RBTreeNode<T> findParentNode(RBTreeNode<T> node) {
RBTreeNode<T> parent = root;
RBTreeNode<T> child = root;
while (child != null) {
int result = child.getValue().compareTo(node.getValue());
if (result == 0) {
// 和其中一只节点相同
return child;
}
parent = child;
if (result > 0) {
child = child.getLeft();
} else {
child = child.getRight();
}
}
return parent;
}
/**
* 找到叔叔节点
*
* @param node node
* @return uncle
*/
public RBTreeNode<T> getUncle(RBTreeNode<T> node) {
RBTreeNode<T> parent = node.getParent();
RBTreeNode<T> grandfather = parent.getParent();
if (grandfather == null) {
return null;
}
if (parent == grandfather.getLeft()) {
return grandfather.getRight();
} else {
return grandfather.getLeft();
}
}
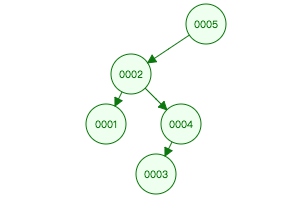
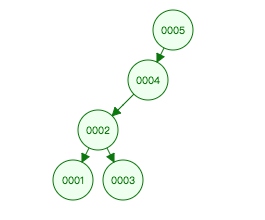图 2.6
图上，对2节点左旋：右节点4替换2，2作为4左节点，3作为2右节点。
/**
* 左旋
*
* @param node node
*/
private void rotateLeft(RBTreeNode<T> node) {
// 把待替换节(n)的右节点(r)替换它
RBTreeNode<T> replaceNode = node.getRight();
node.setRight(replaceNode.getLeft());
if (replaceNode.getLeft() != null) {
replaceNode.getLeft().setParent(node);
}
// r.p = n.p
replaceNode.setParent(node.getParent());
if (node.getParent() == null) {
// p = null, 就是根节点
root = replaceNode;
} else {
// p 重置子节点
if (node.getParent().getLeft() == node) {
node.getParent().setLeft(replaceNode);
} else {
node.getParent().setRight(replaceNode);
}
}
// r.l = n
replaceNode.setLeft(node);
// n.p = r
node.setParent(replaceNode);
}
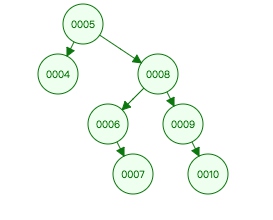
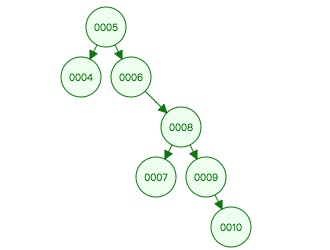图 2.7
/**
* 右旋
*
* @param node node
*/
private void rotateRight(RBTreeNode<T> node) {
// 把待替换节(n)的左节点(l)替换它
RBTreeNode<T> replaceNode = node.getLeft();
RBTreeNode<T> parent = node.getParent();
node.setLeft(replaceNode.getRight());
setParent(replaceNode.getRight(), node);
replaceNode.setRight(node);
setParent(node, replaceNode);
if (parent == null) {
root = replaceNode;
setParent(replaceNode, null);
} else {
if (parent.getLeft() == node) {
parent.setLeft(replaceNode);
} else {
parent.setRight(replaceNode);
}
setParent(replaceNode, parent);
}
}
根据以上情况和方法，插入就变得容易了。
public T addNode(T value) {
RBTreeNode<T> t = new RBTreeNode<T>(value);
return addNode(t);
}
/**
* 插入节点
*
* @param node node
* @return value
*/
private T addNode(RBTreeNode<T> node) {
// 新插入的节点为红色
node.setLeft(null);
node.setRight(null);
node.setRed(true);
if (root == null) {
// 新插入节点为根节点
root = node;
root.setRed(false);
return root.getValue();
}
// 找到要插入的父节点
RBTreeNode<T> parentNode = findParentNode(node);
int result = parentNode.getValue().compareTo(node.getValue());
if (result == 0) {
return node.getValue();
}
if (result > 0) {
parentNode.setLeft(node);
} else {
parentNode.setRight(node);
}
node.setParent(parentNode);
if (parentNode.isRed()) {
fixAdd(node);
}
return null;
}
修复插入后的树
/**
* 插入修复
*
* @param node node
*/
private void fixAdd(RBTreeNode<T> node) {
// 找到parent和uncle
RBTreeNode<T> parent = node.getParent();
while (parent != null && parent.isRed()) {
RBTreeNode<T> uncle = getUncle(node);
if (uncle == null || !uncle.isRed()) {
// 祖先
RBTreeNode<T> ancestor = parent.getParent();
if (ancestor == null) {
parent.setRed(false);
return;
}
if (ancestor.getLeft() == parent) {
boolean isRight = node == parent.getRight();
if (isRight) {
// 左旋，就变成一条斜线
rotateLeft(parent);
}
// 一条斜线，右旋
rotateRight(ancestor);
switchColor(ancestor, ancestor.getParent());
parent = null;
} else {
boolean isLeft = node == parent.getLeft();
if (isLeft) {
rotateRight(parent);
}
rotateLeft(ancestor);
if (isLeft) {
node.setRed(false);
parent = null;
} else {
parent.setRed(false);
}
ancestor.setRed(true);
}
} else if (uncle.isRed()) {
// 1. 叔叔不为空
uncle.setRed(false);
parent.setRed(false);
parent.getParent().setRed(true);
node = parent.getParent();
parent = node.getParent();
}
}
getRoot().setRed(false);
getRoot().setParent(null);
}
三、删除
删除是红黑树最复杂的操作，为避免不被各种情况绕晕，中心思想就是：按照二叉查找树方式删节点，考虑各种情况下是否违背红黑树特性，特别是特性4，5。
这里要做一个重要的说明，是后续删除操作都和这个说明有关： 对于一颗二叉查找树，如果节点有两个孩子，将会找右边子树中最小值(或左边最大值)作为替代值。然后再删除替代值原先的位置。这个替代值一定最多有一个孩子。
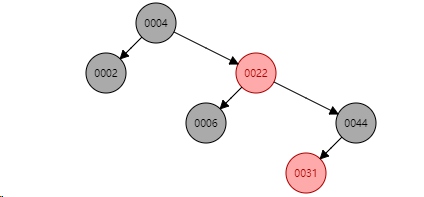
图 3.1
如图3.1, 删除22，替代值将会是31(右子树最小值)，31的左子树一定为空，否则他不会作为替代值。这样看来，二叉树最终操作的是最多有一个孩子的节点。这对红黑树删除操作有很多简化，因为如果有寻找替换节点的过程，只是替换值，并不影响二叉树任何性质。
因此，我们只需要讨论删除只有一个儿子的节点(如果都为叶子节点，可将任意一个作为儿子看待)。
3.1 被删除节点是红色
还是图3.1，节点31为红色，那他的孩子一定都是叶子节点，并不破坏红黑树任何属性(平衡)，直接删除即可。
3.2 被删除节点是黑色，儿子为红色
此时，儿子顶上来，变为黑色，黑色节点没少，也不会破坏特性4，5。
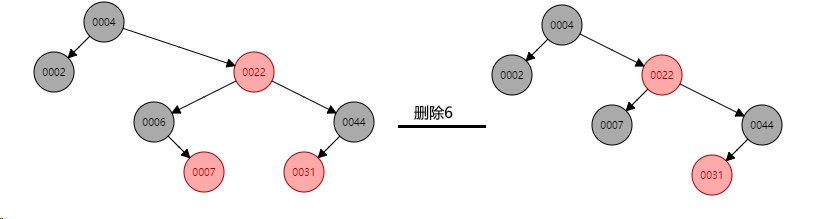图 3.2
3.3 被删除节点是黑色，儿子也是黑色
这种情况较复杂，我们分成多个case处理：
case1： 被删除的是根节点，替换后无需处理。
case2： S节点为红色
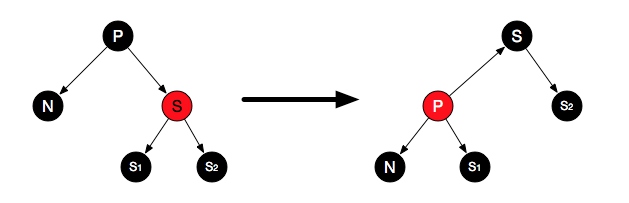图 3.3
图中N为删除后的替换上来的子节点，此时，P-N这个分支已经少了一个黑色节点，其实，S应该是N的叔叔节点, 后续几种case的图也类似表达。
因为兄弟为红色，P和S1、S2坑一定都为黑色。这种情况下，对P左旋，并交换N父亲和祖父颜色。为什么这样做？相对P这个位置，颜色没变，右子树少一个红色节点，并不破坏红黑树性质；对于左子树，S-P-S1 路线上的黑色节点还是没变，对N，还是如同新替换上来的节点，继续做后面几种case处理。
case3：P,S,S1,S2都是黑色
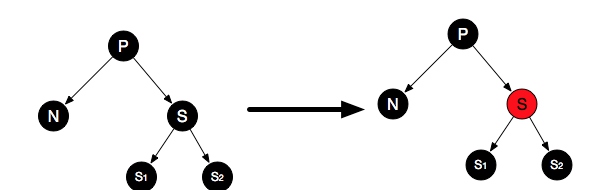图 3.4
如上图左，都为黑色，只需要把兄弟S变为红色即可做到P的作为分支平衡，但是对整个P这条分支，少了一个黑色节点。需要对P重新作平衡处理(从case1开始适配)。
case4：P为红色，S和儿子都不是红色
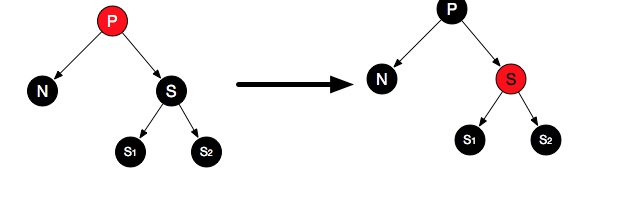图 3.5
这中情况比较简单,把父兄颜色交换即可。因为通过S路径黑色没少，但通过N增加一个黑色P，从而达到平衡。
case5：S是黑色，S的一侧(N同侧)儿子红，另一侧儿子为黑色
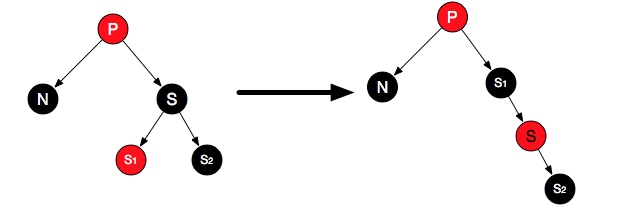图 3.6
这种情况，对S右旋。替换S和新父亲颜色，整个P的右子树黑色简单都没变，但经过N的路线还是少一个黑节点。按case6进行操作
case6：S是黑色，另一侧儿子为红色
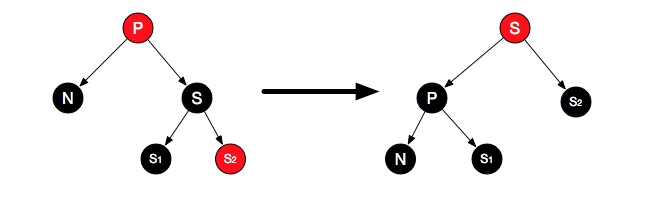图 3.7
如图，对P左旋并和S交互颜色，再把S2变为黑色。这样操作后，最顶上颜色没变，右侧少一个黑色S被S2补充，也没破坏平衡。左侧新增一个黑色节点，从而达到平衡：
注: 这种情况下，P是红色或者黑色都一样。如果图中P为黑色，那么交互颜色后，在此基础上，还还是多了一个黑色祖先(S)
实现
/**
* 删除节点
*
* @param node node
*/
private void remove(RBTreeNode<T> node) {
RBTreeNode<T> dataRoot = getRoot();
RBTreeNode<T> parent = root;
while (dataRoot != null) {
int cmp = dataRoot.getValue().compareTo(node.getValue());
if (cmp < 0) {
// 遍历右子树
parent = dataRoot;
dataRoot = dataRoot.getRight();
} else if (cmp > 0) {
// 遍历左子树
parent = dataRoot;
dataRoot = dataRoot.getLeft();
} else {
// 找到对应节点
if (dataRoot.getRight() != null && dataRoot.getLeft() != null) {
// 被删除节点的"左右孩子都不为空"的情况
RBTreeNode<T> successor = findMin(dataRoot.getRight());
dataRoot.setValue(successor.getValue());
node = successor;
dataRoot = dataRoot.getRight();
} else {
// 最多只有一个孩子
if (dataRoot.isRed()) {
// 两个节点不是非空且是红色，那么孩子一定都是叶子节点
if (parent.getLeft() == dataRoot) {
parent.setLeft(null);
} else {
parent.setRight(null);
}
dataRoot = dataRoot.getLeft() == null ? dataRoot.getRight() : dataRoot.getLeft();
} else {
// 最多只有一个孩子的黑色节点：1. 孩子是红色，2. 没有孩子(叶子节点)
RBTreeNode<T> onlyChild = findOneChild(dataRoot);
if (isRed(onlyChild)) {
//1. 孩子是红色
dataRoot.setValue(onlyChild.getValue());
if (dataRoot.getLeft() == onlyChild) {
dataRoot.setLeft(null);
} else {
dataRoot.setRight(null);
}
return;
}
// 2. 没有孩子(都是叶子节点)
fixRemove(dataRoot);
parent = dataRoot.getParent();
if (parent == null) {
root = null;
return;
}
if (parent.getLeft() == dataRoot) {
parent.setLeft(null);
} else {
parent.setRight(null);
}
dataRoot = null;
}
}
}
}
}
删除修复
/**
* 删除修复
*
* @param node node
*/
private void fixRemove(RBTreeNode<T> node) {
if (node == null || node.isRed()) {
throw new IllegalArgumentException("Node err ... ");
}
RBTreeNode<T> onlyChild = findOneChild(node);
if (isRed(onlyChild)) {
throw new IllegalArgumentException("Node err ... ");
} else {
// 删除节点是黑色，儿子也是黑色(其实应该说孩子都是叶子节点)
RBTreeNode<T> parent = node.getParent();
if (parent == null) {
// case1: 被删除的是根节点，替换后无需处理。
return;
}
boolean isLeft = parent.getLeft() == node;
RBTreeNode<T> sibling = getSibling(node);
if (sibling == null) {
// 黑色(非叶子节点)节点才修改，但黑色节点一定有兄弟
throw new IllegalArgumentException("Node err ... ");
}
if (isRed(sibling)) {
// case2: S节点为红色
if (isLeft) {
rotateLeft(parent);
} else {
rotateRight(parent);
}
switchColor(parent, parent.getParent());
// 此时，新节点还是原来位置
parent = node.getParent();
sibling = getSibling(node);
}
if (!parent.isRed() && !isRed(sibling) && !isRed(sibling.getLeft()) && !isRed(sibling.getRight())) {
// case3: P,S,S1,S2都是黑色
sibling.setRed(true);
if (parent.getParent() == null) {
parent.setRed(false);
} else {
fixRemove(parent);
}
}
if (isRed(parent) && !isRed(sibling.getLeft()) && !isRed(sibling.getRight())) {
//case4： P为红色，S（一定黑）和儿子都不是红色
switchColor(parent, sibling);
return;
}
if (isLeft && !isRed(sibling) && isRed(sibling.getLeft()) && !isRed(sibling.getRight())) {
//case5： S是黑色，S的一侧(N同侧)儿子黑色，另一侧儿子为红色
rotateRight(sibling);
switchColor(sibling, sibling.getParent());
sibling = getSibling(node);
} else if (!isLeft && !isRed(sibling) && isRed(sibling.getRight()) && !isRed(sibling.getLeft())) {
rotateLeft(sibling);
switchColor(sibling, sibling.getParent());
sibling = getSibling(node);
}
// case6: S是黑色，S的一侧(N同侧)儿子黑色，另一侧儿子为红色
if (isLeft && !isRed(sibling) && isRed(sibling.getRight())) {
rotateLeft(parent);
sibling.getRight().setRed(false);
switchColor(parent, sibling);
} else if (!isLeft && !isRed(sibling) && isRed(sibling.getLeft())) {
rotateRight(parent);
sibling.getLeft().setRed(false);
switchColor(parent, sibling);
}
}
}
省略了一些方法如switchColor,getSibling。代码还有不少可以重构优化的点。源码
参考文档: [1]. https://zh.wikipedia.org/wiki/%E7%BA%A2%E9%BB%91%E6%A0%91 [2]. http://sandbox.runjs.cn/show/2nngvn8w [3]. https://tech.meituan.com/redblack-tree.html [4]. http://blog.csdn.net/v_JULY_v/article/details/6284050 [5]. https://www.cs.usfca.edu/~galles/visualization/RedBlack.html [6]. https://github.com/julycoding/The-Art-Of-Programming-By-July/blob/master/ebook/zh/03.01.md